Finalmente, presentaremos un resultado numérico basado en una simulación de un reservorio cuántico concreto, aplicado a la tarea de predecir una serie temporal caótica en tres dimensiones. Aunque no entraremos en detalle sobre el funcionamiento del sistema cuántico, este ejemplo será útil para ver que estas novedosas redes neuronales cuánticas son capaces de realizar tareas realmente complejas

1. El mundo cuántico

La mecánica cuántica es una rama de la física que estudia el comportamiento de los sistemas a escalas extremadamente pequeñas, entre 10^-10 y 10^-15 metros, donde las interacciones entre los electrones y el núcleo de los átomos es apreciable. Comenzó a formalizarse a principios del siglo XX con avances como la solución de Max Planck a la “catástrofe del ultravioleta” y el descubrimiento del efecto fotoeléctrico por Albert Einstein. No obstante, fue en la reunión de Copenhague en 1927 cuando científicos como Niels Bohr, Erwin Schrödinger, Marie Curie, Paul Dirac y Max Planck, entre otros, establecieron los principios fundamentales de la mecánica cuántica.

El término “cuántica” proviene del concepto de “cuanto”, introducido por Max Planck en 1900. Planck sugirió que, en ciertos contextos, la energía se transmite en “paquetes” discretos, en lugar de hacerlo de manera continua. Un cuanto de energía es ese paquete mínimo que puede transferirse. Este concepto aparece en fenómenos como el efecto fotoeléctrico y en la resolución de la ecuación de Schrödinger en diversos sistemas cuánticos. Cuando la energía está “cuantizada”, solo puede tomar valores específicos, no un rango continuo. Un buen ejemplo sería imaginar que en una tienda solo venden pelotas de tenis en paquetes de tres. Se pueden comprar 3, 6 o 9 pelotas, pero no 4 ni fracciones como 4.34 pelotas. De forma similar, los “cuantos” son las unidades mínimas de energía permitidas en un sistema cuántico, y no se puede adquirir energía más allá de lo que estos paquetes permiten.

Sin embargo, esta no es ni mucho menos la única peculiaridad de la mecánica cuántica. Para revisar y comprender todas sus propiedades con precisión, se necesita utilizar un formalismo matemático conocido como espacios de Hilbert, que son espacios vectoriales empleados para describir los sistemas físicos cuánticos, y constituyen una herramienta clave en este campo. No obstante, en nuestro caso, nos limitaremos a explicar las ideas principales de manera cualitativa, ya que el formalismo matemático implicaría un estudio más extenso y detallado. A continuación, destacamos algunas de estas propiedades.

1.1. Estados Cuánticos y Superposición

Dado un sistema físico cuántico, los posibles estados del sistema pueden representarse como una superposición de diferentes estados. Esto significa que el sistema puede estar en varios estados a la vez, pero cada uno tiene un coeficiente asociado que determina la probabilidad de obtener ese estado cuando lo medimos. Es decir, un sistema físico cuántico puede estar en varios estados al mismo tiempo, pero al medirlo obtenemos el resultado que corresponde a uno de ellos con su probabilidad. Este fenómeno, en el que al medir el sistema el estado cuántico “va” a uno de sus posibles estados involucrados en la superposición, se suele denominar como que el estado cuántico ha colapsado al estado de la medición.

Para entenderlo mejor, imaginemos que describimos a un deportista de triatlón como un sistema cuántico con tres posibles estados: nadando, corriendo y haciendo bici. De manera general, el estado cuántico del deportista sería una superposición de estos tres: estaría nadando, corriendo y haciendo bici a la vez, con una cierta probabilidad para cada actividad. La peculiaridad es que, al intentar observar qué está haciendo el deportista (o medir su estado), solo lo veremos realizando una de las tres actividades, y cuál sea dependerá de las probabilidades asociadas a cada estado. Si las probabilidades fueran 0.3, 0.5 y 0.2 para nadar, correr y hacer bici respectivamente, esto significa que, en principio, de 100 mediciones, esperaríamos encontrar al deportista nadando 30 veces, corriendo 50 veces y haciendo bici 20 veces. Esto refleja cómo, en un sistema cuántico, la probabilidad asociada a cada estado determina la frecuencia con la que ese estado se manifestará al realizar múltiples mediciones. Esto también está ejemplificado en la Figura 1, con el tradicional caso del gato de Schrödinger.

Por tanto, vemos que la mecánica cuántica es intrínsecamente estadística, ya que antes de una medición solo podemos conocer las probabilidades de los posibles resultados, no el resultado exacto. Este enfoque probabilístico generó controversia, ya que desafiaba el determinismo tradicional, donde conocer todos los parámetros de un sistema permite predecir su comportamiento. Einstein fue uno de sus principales críticos, manifestando su escepticismo con la famosa frase “Dios no juega a los dados”. A pesar de las críticas, la mecánica cuántica ha demostrado ser capaz de explicar con precisión numerosos experimentos.

1.2. Observables Físicos e Incertidumbre

En mecánica cuántica, los observables físicos se representan mediante operadores matemáticos que actúan sobre el estado cuántico del sistema. Un ejemplo común es el operador de energía (Hamiltoniano del sistema), que determina los posibles valores de energía, a menudo cuantizados. Lo peculiar de la cuántica es que algunos observables no son compatibles, lo que significa que no se pueden medir simultáneamente con precisión. Un ejemplo es el principio de incertidumbre de Heisenberg, que indica que no es posible conocer con exactitud tanto la posición como el momento de una partícula al mismo tiempo.

Para ilustrarlo, imagina que has quedado con un amigo para cenar (amigo A), pero al mismo tiempo otro amigo (amigo B) quiere hablar contigo urgentemente por teléfono. Ambos tienen mensajes muy importantes para ti, pero solo puedes escuchar a uno. Si decides prestar atención exclusivamente a A, sabrás perfectamente lo que él quiere decir, mientras que no sabrás nada del mensaje de B, y viceversa. También podrías intentar escuchar a ambos a la vez, pero eso haría que captaras algo de los dos mensajes, aunque sin precisión en ninguno. No podrías conocer ninguno de los mensajes completamente. Este dilema no surge porque seas “malo” prestando atención, sino por una limitación física de tu capacidad para escuchar a ambos a la vez. Algo muy similar sucede en la mecánica cuántica con observables incompatibles: no podemos conocer sus valores con precisión simultáneamente, debido a la naturaleza física de los mismos.

1.3 Entrelazamiento Cuántico

Por último, vamos a comentar otra peculiaridad más de los sistemas cuánticos a la que no estamos acostumbrados: el entrelazamiento cuántico. Este fenómeno se presenta en sistemas cuánticos compuestos por varios subsistemas, es decir, cuando existen varias partículas que interactúan entre sí. Para simplificar el problema, pensemos en dos partículas, cada una con sus propios estados cuánticos, los cuales no tienen por qué ser iguales o estar relacionados de manera obvia.

Cuando se dice que ambas partículas están entrelazadas, significa que no se puede describir el estado cuántico de cada una por separado, sino solo a través de un estado cuántico global. Esto implica que el estado de una partícula depende del estado de la otra, por lo que no se puede conocer el estado de una sin referirse al de la otra. Por ejemplo, si tú y tu mejor amigo/a estuvieran entrelazados cuánticamente, cualquier pensamiento o acción de uno afectaría directamente al otro. Así, en lugar de actuar de manera independiente, estaríais tan interconectados que no podríais consideraros como dos entidades separadas, sino como un solo conjunto. Esto refleja la esencia del entrelazamiento cuántico, donde el comportamiento de uno está inseparablemente vinculado al del otro, sin importar la distancia entre vosotros.

Como hemos comentado, el entrelazamiento cuántico va más allá de lo que observamos en la física clásica, donde cada objeto o partícula tiene un estado independiente y bien definido. Esto implica que dos partículas entrelazadas, aunque estén separadas por miles de kilómetros, se “comunican” instantáneamente al ser medida una de ellas, lo que provoca el colapso del estado de la otra. Albert Einstein denominó a esto “acción espeluznante a distancia”, ya que parecía que las partículas entrelazadas podían influirse instantáneamente, sin importar la distancia que las separase. Sin embargo, hoy sabemos que el entrelazamiento cuántico ha sido experimentalmente comprobado y tiene aplicaciones clave en tecnologías como la computación cuántica y la criptografía cuántica.

2. Medición de Observables: Valores Promedio

Ya hemos discutido algunos de los aspectos más controvertidos de la mecánica cuántica, como la superposición, la existencia de observables físicos no compatibles y el entrelazamiento cuántico. Sin embargo, dado que la cuántica es inherentemente probabilística, surge la pregunta: ¿cómo podemos asignar un valor concreto a un observable si el resultado de cada medición es aleatorio? La respuesta a esta cuestión es que se utilizan valores promedio.

Para entender mejor esta idea, vamos a hacer una analogía comparando la medición en física cuántica con la experiencia de ser autónomo en España. La primera cualidad que tienen en común estas dos situaciones aparentemente diferentes es que ambas son complicadas. Sin embargo, lo que nos interesa es entender que los ingresos de un autónomo pueden variar de mes a mes. Por ejemplo, si tenemos un negocio de joyería, en diciembre las ventas serán mucho mayores debido a la Navidad, o en febrero por San Valentín. La cuestión es que algunos meses se ganará más dinero que otros. Entonces, ¿cuál sería el salario mensual promedio de un autónomo en este caso? La opción más obvia para calcular esto sería sumar todas las ganancias anuales y dividirlas entre los 12 meses, lo que nos daría el promedio mensual de ingresos. Este sencillo cálculo es equivalente a multiplicar las ganancias de cada mes por la probabilidad de haber ganado esa cantidad ese mes.

De manera análoga, en mecánica cuántica, cuando intentamos definir el valor de un observable, usamos el promedio (también denominado valor esperado) para hacer referencia a una cantidad física. Este promedio no es exacto debido a la naturaleza probabilística de los sistemas cuánticos, lo que significa que siempre llevará asociada una incertidumbre. Esa incertidumbre se puede calcular mediante otros promedios más complicados, los cuales nos dan una medida de la dispersión de los valores posibles. En este contexto, el principio de incertidumbre de Heisenberg juega un papel crucial, ya que establece una relación entre estas incertidumbres en el caso de que los operadores no sean compatibles, como hemos discutido anteriormente.

3. Aprendizaje Automático Cuántico

Ahora que ya hemos repasado algunos de los conceptos más controvertidos y claves de la mecánica cuántica, vamos a discutir un poco sobre una nueva rama tecnología que intenta combinar las capacidades del aprendizaje automático (machine learning) y la cuántica, conocida en inglés como quantum machine learning. En particular, nuestro interés se centrará en la computación cuántica de reservorio (quantum reservoir computing), que consiste en la versión cuántica del modelo de red neuronal que discutimos en el anterior post “Prediciendo el Caos”.

Este nuevo campo fue propuesto por primera vez en 2017 Harnessing Disordered-Ensemble Quantum Dynamics for Machine Learning y está siendo ampliamente investigado en los últimos años. Sin embargo, este modelo no es el único tipo de aprendizaje automático cuántico en desarrollo. Existen otros enfoques, de los que no hablaremos en este texto,basados en la computación cuántica con circuitos cuánticos variacionales.

A modo de recordatorio, la computación de reservorio (reservoir computing) hace referencia a un tipo particular de red neuronal artificial que utiliza un sistema dinámico para procesar la información de los datos de entrada y producir un resultado. Para lograr esto, la red tiene que ser previamente entrenada como en cualquier modelo de aprendizaje automático. Por ejemplo, en el anterior post vimos que una red neuronal de este tipo ere capaz de predecir series temporales caóticas, una tarea realmente desafiante.

La computación cuántica de reservorio consiste en utilizar los mismos principios, con la peculiaridad de que el sistema dinámico se trata de un sistema físico cuántico. El objetivo de este sistema cuántico es procesar la información para realizar diversas tareas. De esta forma, se pueden destacar tres pasos claves para lograr esto:

• Primero, es necesario un método para codificar los datos de entrada en estados cuánticos del sistema, de manera que el reservorio cuántico los pueda procesar adecuadamente. Esto se hace codificando la información en estados en superposición cuántica, lo que puede variar mucho según el sistema físico que se esté empleando.
• Segundo, se requiere de una dinámica cuántica suficientemente compleja para dar lugar a las propiedades que debe tener cualquier reservorio para funcionar correctamente. Esto es, el sistema cuántico debe proveer de memoria a la red neuronal, a la vez que no linealidad, para ser capaz de aprender los patrones ocultos en los datos de entrada.
• Por último, es necesario una serie de observables físicos cuánticos que constituyen la salida del reservorio. Estos observables se miden utilizando el valor medio, como hemos comentado anteriormente. Para poder entrenar el reservorio cuántico, es necesario que haya, en general, muchos observables que medir a la salida.

Sin embargo, ¿cuál es el objetivo de estas redes neuronales cuánticas si ya tenemos modelos muy avanzados que funcionan bien en ordenadores digitales? La respuesta es intentar mejorar la eficiencia de estos modelos explotando las propiedades de la cuántica, tales como la superposición de estados cuánticos o el entrelazamiento, entre otras. Los modelos actuales son muy costosos en términos de recursos computacionales y enfrentan problemas de escalabilidad a medida que se incrementa la complejidad de las tareas. Por otro lado, el reto en quantum reservoir computing es trabajar con estos sistemas cuánticos, ya que su implementación experimental es realmente compleja y representa una de las principales barreras que se intenta superar actualmente para avanzar en el campo.

4. Resultados Numéricos

En este último apartado, exploraremos la capacidad de un nuevo modelo de reservorio cuántico en el que he trabajado junto a mis supervisores durante mi tesis de máster. Este reservorio utiliza quantum memristors, un tipo de resistencia con memoria. El término memristor proviene de la combinación de las palabras memoria y resistor (resistencia en inglés). El objetivo es desarrollar una implementación cuántica de estos memristors y utilizarlos como reservorio. Esta idea se inspira en un artículo científico en el que, hace unos años, un equipo experimental de la Universidad de Viena demostró que era posible crear quantum memristors de forma experimental con una plataforma fotónica Experimental photonic quantum memristor.

En nuestra primera propuesta con estos dispositivos, el reservorio consiste en utilizar varios de los quantum memristors para procesar la información. Estos dispositivos tienen una entrada de información y generan valores de salida, que se emplean como el output del reservorio. Cada uno de ellos tiene una configuración específica y algunos parámetros que permiten modificar la dinámica del reservorio. Estos parámetros se pueden ajustar, dando lugar a comportamientos diversos y permitiendo realizar diferentes tareas. Cabe recalcar que, aunque el objetivo final sea la implementación experimental de este reservorio cuántico, por el momento se ha realizado un estudio numérico de su potencial. Por lo tanto, los resultados corresponden a simulaciones llevadas a cabo en un ordenador digital.

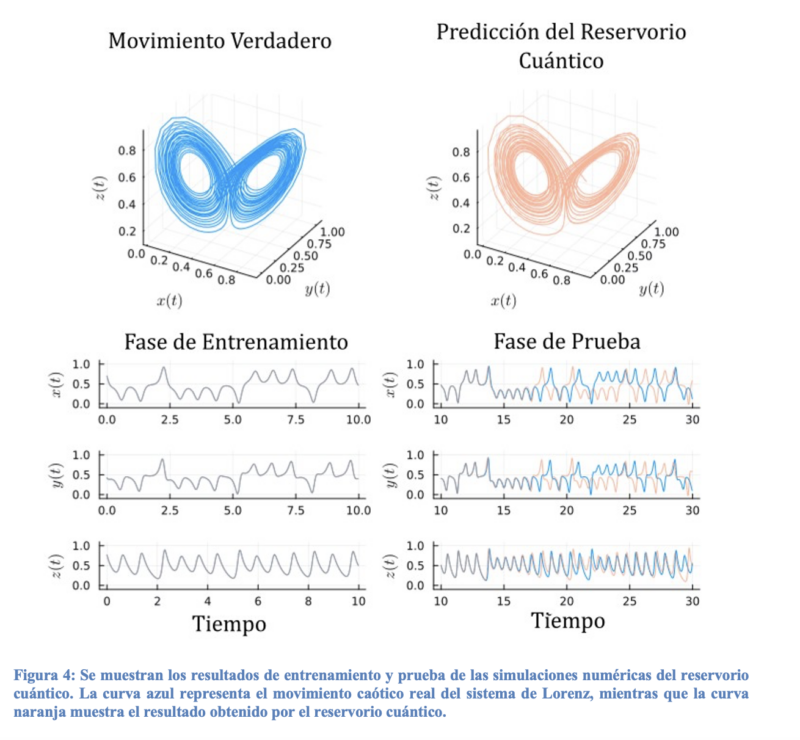
En este caso, mostramos un ejemplo de predicción de una serie temporal caótica. Esta tarea es similar a la discutida en el post anterior; para más detalles sobre el caos, recomiendo consultarlo. La predicción se realiza sobre las tres coordenadas dependientes del tiempo: x(t), y(t) y z(t), correspondientes al sistema de Lorenz. Este sistema dinámico en tres dimensiones fue propuesto en 1963 por Edward Lorenz como un modelo para describir ciertas dinámicas atmosféricas.

De esta forma, se introduce en el reservorio cuántico la serie temporal tridimensional, apropiadamente codificada en un estado cuántico en superposición, para su procesamiento. Los quantum memristors generan un output que corresponde al valor promedio de un observable físico cuántico, en este caso, el valor medio de fotones en la salida del dispositivo. Con este output, se entrena una capa clásica de salida para obtener finalmente el valor de la predicción de la serie. Los resultados de este proceso se muestran en la Figura 3, donde se puede observar la fase completa de entrenamiento, en la que el reservorio y el movimiento real son prácticamente iguales, por lo que se ven superpuestos, y la fase de prueba. En esta última, se observa que al principio la predicción es realmente buena, pero, al pasar un poco de tiempo, el reservorio comienza a fallar. En cualquier caso, si representamos la trayectoria completa en un espacio tridimensional (parte superior de la gráfica), se puede ver que el movimiento global predicho es muy similar al verdadero, lo que indica que el reservorio está aprendiendo la dinámica del sistema de Lorenz de manera correcta. Recordemos que esta es una tarea difícil, ya que el caos se caracteriza por el hecho de que un cambio casi imperceptible al inicio de una trayectoria puede dar lugar a movimientos completamente diferentes (efecto mariposa).

5. Conclusiones

Hemos discutido de forma cualitativa algunas de las propiedades clave y peculiares de la mecánica cuántica, como la superposición cuántica, el entrelazamiento y la medición de observables físicos. Posteriormente, hemos abordado los fundamentos del quantum reservoir computing, una nueva rama propuesta por primera vez en 2017 Harnessing Disordered-Ensemble Quantum Dynamics for Machine Learning. Finalmente, hemos explorado el potencial de un modelo específico de reservorio cuántico utilizando quantum memristors (resistencias cuánticas con memoria) para realizar tareas complejas. En particular, las simulaciones indican que el sistema cuántico sería capaz de predecir una dinámica caótica tridimensional, lo que representa una tarea realmente compleja.

El campo de quantum reservoir computing es realmente joven, pero ha recibido mucha atención en los últimos años, en los que se han hecho diversas propuestas teóricas para posibles reservorios cuánticos. Sin embargo, los experimentos en el campo no son tan abundantes debido a las complicaciones que presenta la cuántica, pero este año se han publicado las primeras implementaciones reales en distintos dispositivos. Por ejemplo, hace unos meses, la empresa QuEra, dedicada a la computación cuántica con átomos neutros, publicó un artículo en el que presentó resultados experimentales con un reservorio cuántico basado en esta tecnología Large-scale quantum reservoir learning with an analog quantum computer.

Sin embargo, aún queda mucho por investigar para establecer de manera clara las ventajas que pueden ofrecer estos reservorios cuánticos. El objetivo final de estas implementaciones es desarrollar redes neuronales más eficientes que aprovechen las propiedades cuánticas de la materia para mejorar sus capacidades. Aún queda un largo camino por recorrer en este nuevo campo de investigación, y esto es solo el comienzo.

Bibliografía