Colaboración especial de Daniel Montesinos Capacete. Becario Sicómoro en el Master de Física de los Sistemas Complejos del IFISC (UIB-CSIC) curso 2023-2024.
Introducción
El siglo XX fue indudablemente la era de la física, marcada por una gran cantidad de avances científicos que transformaron nuestro entendimiento del universo. Desde la mecánica cuántica y la relatividad general de Einstein hasta teorías aún más complejas, estos logros sentaron las bases para el desarrollo de tecnologías que hoy consideramos cotidianas, como computadoras, teléfonos móviles y GPS. Ahora, en el primer cuarto del siglo XXI, nos enfrentamos a la pregunta: ¿Cuál será la próxima disciplina científica que revolucionará nuestro mundo? Muchos argumentarían que estamos en la era de los algoritmos y, sobre todo, de la Inteligencia Artificial (IA).
Los algoritmos son secuencias de instrucciones que pueden programarse en computadoras para realizar diversas funciones. Aunque la física utiliza algoritmos en forma de simulaciones para estudiar sistemas complejos, la verdadera protagonista de esta época es la IA. Es probable que hayas escuchado sobre la IA en redes sociales o navegando por internet, tal vez advirtiendo sobre el temor a la pérdida de empleos debido a ella. La IA es una tecnología prometedora que, en muchos casos, puede superar las capacidades humanas en tareas específicas. A pesar de su rápido avance, entender cómo funcionan estos modelos y lograr que operen de manera efectiva puede resultar desafiante.
Existen diversas formas de modelar la IA, pero todos los modelos comparten una idea fundamental: replicar las capacidades del cerebro humano. En esta exploración, no nos centramos en comprender los grandes modelos de lenguaje como ChatGPT, sino en los fundamentos en los que se basan. ¿Cuál es la unidad mínima que procesa la información en estos sistemas sofisticados? ¿Cómo distinguen entre textos e imágenes? Estas preguntas nos conducen al corazón de la IA: las redes neuronales.

Las redes neuronales son la piedra angular del deep learning (aprendizaje profundo), una rama de la IA que ha experimentado un crecimiento exponencial en los últimos años y que va mas allá del machine learning (aprendizaje automático). El diseño de estas redes es un arte en sí mismo, ya que no hay una sola forma de construirlas. Para comprender su funcionamiento, vamos a explorar cómo se entrena y se prueba un modelo específico de red neuronal llamado Echo State Network (ESN). Utilizaremos esta red para predecir series temporales caóticas, lo que nos permitirá vislumbrar el potencial de las redes neuronales en acción. Entonces, trabajaremos dos conceptos en principio independientes que son el caos y el machine learning. El objetivo es entender cómo es posible implementar y entrenar redes neuronales para resolver tareas complejas como la predicción de un movimiento caótico. Para ello, primero hablaremos sobre cómo se mide el caos para después hablar en detalle sobre nuestra red neuronal.
¿Qué es el Caos?
Para entender formalmente el concepto de caos, debemos olvidar por completo la idea intuitiva de que caos se corresponde con desorden. Es decir, cuando decimos que una serie temporal es caótica, no es correcto pensar en algo aleatorio o desordenado. Imagina un péndulo. Cuando lo dejamos oscilar desde una posición inicial, su movimiento sigue un patrón predecible. Sin embargo, si acoplamos más péndulos o fuerzas variables, su comportamiento se vuelve más complicado, de tal forma que pequeñas variaciones dan lugar a movimientos y patrones de movimiento distintos. De hecho, el péndulo doble es uno de los sistemas más simples que experimentan comportamiento caótico.
El caos se presenta en sistemas dinámicos complejos cuando pequeñas diferencias en las condiciones iniciales conducen a resultados completamente diferentes con el tiempo. Esto significa que si tenemos dos péndulos dobles y los colocamos en una posición inicial aparentemente igual para nuestros ojos, su trayectoria va a ser muy diferente debido a cualquier pequeña diferencia que haya en la colocación inicial. Es interesante notar que el caos es determinista, en el sentido de que estos sistemas evolucionan siguiendo unas ecuaciones bien definidas pero que dan lugar a esta peculiaridad debido a la complejidad de las mismas. En simples palabras, conocida exactamente la posición inicial y los parámetros del modelo, el movimiento siempre es el mismo, pero añadir un mínimo cambio da lugar a una trayectoria muy diferente.
Por tanto, vemos que una de las características esenciales del caos es la sensibilidad a las condiciones iníciales del sistema. Ahora podríamos preguntarnos ¿Es posible cuantificar como de caótico es un sistema? La respuesta es afirmativa: usando el coeficiente de Lyapunov. Este coeficiente es un número que mide como de rápido se alejan entre sí las trayectorias cercanas en un sistema dinámico. Imagina dos partículas que inicialmente están muy cerca una de la otra en su trayectoria. Si el sistema es caótico, estas partículas comenzarán a distanciarse rápidamente entre sí con el tiempo, lo que significa que la distancia entre ellas crecerá exponencialmente. El exponente de Lyapunov mide esta tasa de divergencia exponencial. Un exponente positivo indica que las trayectorias se separan exponencialmente, lo que sugiere la presencia de caos en el sistema. Por otro lado, un exponente negativo indica que las trayectorias convergen hacia una solución estable y por tanto el sistema no es caótico.
Nuestro objetivo es intentar entrenar una red neuronal que sea capaz de predecir estas series temporales caóticas. Concretamente, usaremos el sistema de Rössler. Este sistema es un ejemplo clásico de un sistema dinámico que exhibe comportamiento caótico. Fue propuesto por el físico y químico alemán Otto Rössler en 1976 como un modelo simplificado para describir ciertos aspectos del comportamiento caótico en reacciones químicas. Aunque su formulación original fue motivada por la química, el sistema de Rössler se ha convertido en un modelo fundamental en el estudio del caos y ha encontrado aplicaciones en una amplia gama de campos, desde la física hasta la biología y la ingeniería. El sistema de Rössler es tridimensional y su movimiento viene dado por tres ecuaciones diferenciales de la forma:

donde x, y, z son las coordenadas del sistema que representan el movimiento del mismo. Por otro lado, a,b y c son parámetros del sistema que nosotros fijamos. El punto encima de las coordenadas del sistema indica la derivada temporal de la variable correspondiente. En términos simples, cada ecuación nos dice como cambia en el tiempo cada coordenada en función de las demás.
¿Qué son las Redes Neuronales?
Los algoritmos han sido usados para realizar tareas que puedan ser escritas como una serie de instrucciones concretas. De esta forma, los algoritmos se pueden entender como recetas para que los ordenadores realicen cálculos concretos. Sin embargo, no todos los problemas se pueden reducir a una serie de instrucciones. Por ejemplo, ¿cómo enseñarías a un ordenador a distinguir entre distintos tipos de animales? Los humanos tenemos cierta intuición y no dudaríamos entre un distinguir un perro y un lobo, pero enseñar a una maquina a distinguirlos no es tan sencillo ya que tienen rasgos muy similares. Es aquí donde entra el machine learning, como un conjunto de métodos que permiten enseñar tareas que no se pueden reducir a un simple conjunto de instrucciones a seguir. Dentro de estas técnicas, existen distintos tipos de implementaciones, entre ellas las redes neuronales.
Las redes neuronales se inspiran en el funcionamiento del cerebro humano, donde miles de millones de neuronas se comunican entre sí a través de conexiones sinápticas. Del mismo modo, las redes neuronales artificiales están compuestas por unidades de procesamiento llamadas neuronas, organizadas en capas interconectadas. Cada neurona recibe entradas de información, las procesa mediante una cierta función de activación y transmite la salida a las neuronas de la capa siguiente. Existe gran cantidad de formas en las que se pueden conectar estas capas y hay mucha libertad a la hora de elegir como se transmite la información entre ellas. Esto hace que el diseño de redes neuronales sea un campo desafiante y en evolución.
Lo que hace que las redes neuronales sean tan poderosas es su capacidad para aprender a partir de datos. Para ello, deben ser entrenadas con el objetivo de, posteriormente, ser capaces de funcionar autónomamente. En la fase de entrenamiento, se introduce unos datos de entrada a la red neuronal que son procesados y se ajustan unos pesos internos para que la red dé el resultado correcto. Un problema frecuente que se presenta a la hora de entrenar las redes es justamente el tener que ajustar los pesos internos de la misma ya que puede ser una tarea con un coste computacional elevado. Los pesos se pueden ajustar de diferentes formas, luego concretaremos más sobre como lo vamos a hacer con nuestra red.
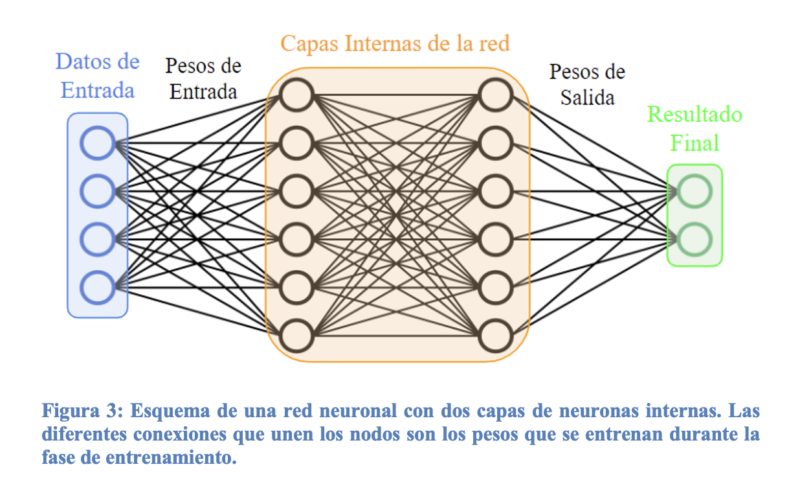
Hemos hablado superficialmente de cómo funciona una red neuronal en general pero entender el motivo de que sean tan buenas es complicado. De hecho, el problema que hay en este sentido es que no se sabe con exactitud como consiguen aprender tan bien y por eso muchas veces se habla de ellas como una caja negra. Sin embargo, se conocen ciertas propiedades características que son esenciales para el aprendizaje de la red: la no linealidad y la expansión multidimensional de los datos de entrada.
Una función lineal es aquella que relaciona dos o más variable siguiendo una recta. Por ejemplo, establece una relación lineal entre ambas variables. Una de las claves del poder de las redes neuronales radica en las funciones de activación no lineales, que son cualquier función que no sea lineal. Algunos ejemplos se pueden ver en la Figura 4. Estas funciones se aplican a la salida de cada neurona y permiten que la red aprenda y represente relaciones complejas y no lineales en los datos. Sin funciones de activación no lineales, una red neuronal solo podría realizar transformaciones lineales de los datos, lo que limitaría su capacidad para aprender y representar patrones complejos.

Reservoir Computing: Echo State Network
En el vasto campo del aprendizaje profundo, el reservoir computing (computación de reservorio) emerge como una técnica innovadora y poderosa para el procesamiento de señales y la realización de tareas de predicción y clasificación. Se trata de un tipo red neuronal que usa un reservorio fijo y de alta dimensionalidad para procesar datos de entrada. El reservorio consiste en un conjunto de unidades de procesamiento recurrentes interconectadas (las neuronas que forman el reservorio), cuyas conexiones se establecen de manera aleatoria y se mantienen fijas durante el proceso de entrenamiento. Esta característica clave permite una implementación eficiente y una capacidad de generalización superior en comparación con otros enfoques ya que reduce en gran medida el número de pesos que hay que ajustar durante el entrenamiento. Dentro de la computación de reservorio, la ESN es un tipo particular de red neuronal que destaca por su simplicidad y eficacia comparada con otros modelos. A continuación explicamos los detalles sobre su implementación.

En primer lugar, se introducen en la red los datos de entrada, que en este caso se trata de una serie temporal que corresponde a algunas de las coordenadas del sistema de Rössler. Esta serie temporal entra a la ESN mediante una matriz de entrada con pesos aleatorios denominada
. Esta información pasa a las neuronas de nuestro reservorio y es procesada mediante una función no lineal. En este caso usamos la tangente hiperbólica. A cada una de las neuronas se le asigna un valor numérico
que representa la activación neuronal de la misma. Por tanto, a cada dato de entrada
a tiempo
, las activaciones neuronales se actualizan siguiendo una tangente hiperbólica. Este proceso también tiene en cuenta las conexiones internas de las neuronas que vienen dadas por otra matriz aleatoria
. Con todos estos ingredientes, el proceso por el que rige la dinámica del reservorio se describe como

donde se puede ver que la activación de las neuronas a tiempo depende del estado de las activaciones al tiempo anterior
. El valor
es el resultado final de la red que se obtiene a partir de la matriz de salida
. Esta matriz es desconocida al principio y el objetivo del entrenamiento es ajustar sus elementos (pesos de salida) para realizar la tarea de predicción que queremos. Esto se hace cuando se ha obtenido una gran cantidad de activaciones neuronales al introducir una serie temporal larga en el reservorio, de manera que los pesos se ajustan para que el resultado de introducir
sea
. Todo este proceso está esquematizado en la Figura 6.
Resultados
Ahora comentaremos como de buena es la predicción que conseguimos con nuestra red neuronal. Para obtener buenas predicciones, es importante encontrar los parámetros globales de la red que funcionen mejor. Esta tarea es realmente complicada ya que, en general, no hay una forma concretar de determinar que parámetros pueden ser los adecuados. De hecho, los parámetros óptimos de la ESN pueden depender de la tarea que se esté realizando. En esta situación, lo más común es utilizar fuerza bruta e ir probando con todos los rangos de valores que creamos que puedan ser convenientes hasta encontrar los valores que parecen dar mejor resultado.
En la Figura 7 se muestra un ejemplo de predicción usando los parámetros óptimos de la ESN. Podemos ver que se consigue una predicción bastante buena y que es capaz de acertar con alta precisión durante un tiempo prolongado. Sin embargo, es importante recordar que la matriz de entrada y la del reservorio están formadas por números aleatorios. Esto significa que para los mismos valores de los parámetros globales, la predicción puede variar debido a esta aleatoriedad. En la figura se muestra una de las mejores predicciones que se obtuvieron con la ESN.
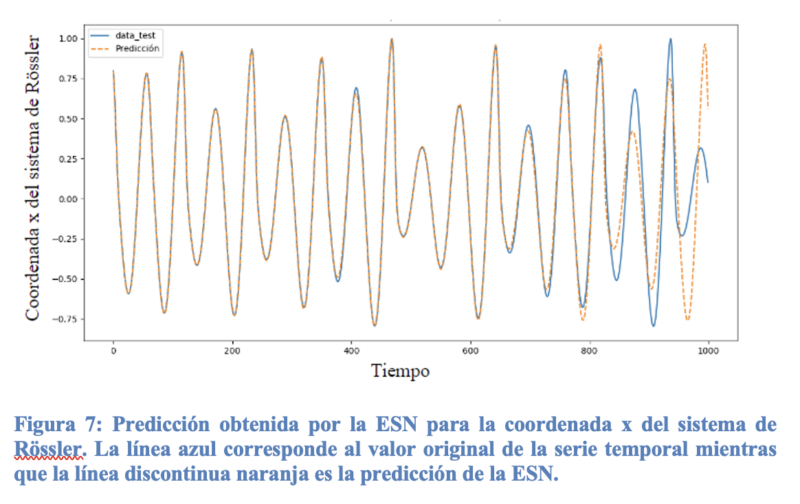
Una forma de intentar entender como la ESN es capaz de predecir, es analizando como es la dinámica interna del reservorio. Es decir, estudiar la evolución temporal de la activación de cada una de las neuronas. De hecho, una pregunta interesante es si ¿está el reservorio imitando de alguna forma el comportamiento caótico de la serie temporal de entrada? Esto se puede estudiar calculando el máximo coeficiente de Lyapunov (MLE) del sistema definido por todo el conjunto de neuronas. La idea se trata de mirar como divergen las trayectorias de las activaciones neuronales debido a pequeñas variaciones, para calcular el MLE y determinar si hay comportamiento caótico en la dinámica del reservorio. Un MLE con valor positivo indica caos mientras que un valor negativo significa que la dinámica no es caótica. Haciendo esto, es posible ver que la mejor predicción se obtiene cuando las neuronas del reservorio se encuentran al borde del caos, pero siguen manteniendo cierta estabilidad. Esto significa que, para mejorar la predicción de series temporales caóticas, hay que usar parámetros de la red que permitan obtener una dinámica interna cercana al caos (su MLE es muy cercano a cero pero sigue siendo negativo).
Conclusión
Hemos discutido conceptos básicos para comprender la idea básica de caos y de red neuronal hasta llegar a la predicción de una serie temporal caótica utilizando una ESN. El resultado más interesante de esto, ha sido ver como la predicción de la ESN es significativamente mejor cuando las neuronas del reservorio tienen un comportamiento casi caótico. Reflexionando sobre este resultado, podemos llegar a la conclusión de que el aprendizaje óptimo se obtiene ajustando la red neuronal de manera que su dinámica no sea muy aburrida (demasiado estable) pero tampoco excesivamente loca (caótica). El aprendizaje es mayor entre estos dos regímenes, justo al borde del caos.
El estudio de redes neuronales y diferentes arquitecturas para las mismas es una rama amplia y que sigue en desarrollo. El estudio del caos en redes neuronales no algo realmente tan sencillo como lo hemos presentado aquí y requiere de matizar ciertos detalles técnicos de los que no hemos hablado. Por eso, no es posible afirmar que en general cualquier red neuronal vaya a mejorar su funcionamiento estando al borde del caos. De hecho, el “estar al borde del caos” es algo que es propiamente difícil de definir de manera precisa en el contexto de redes neuronales.
Dentro del mundo del aprendizaje automático, la computación de reservorio sigue igualmente siendo un campo de investigación. Hay investigaciones recientes en las que se ha estudiado como adaptar este mismo modelo de ESN con reglas de plasticidad sináptica que intenta modelar el funcionamiento del cerebro humano (Guillermo B. Morales, 2021). También hay otros estudios en los que se hace un análisis de la dinámica de la ESN pero siendo entrenada con imágenes para diferentes tareas (Miguel A Muñoz, 2021). Además, existe la posibilidad de implementar este tipo de redes neuronales mediante sistemas físicos como fotones (Mitsumasa Nakajima, 2021).
Existe una variante reciente que va en la línea de la computación cuántica y se denomina computación cuántica de reservorio. En este casi es la idea es implementar la dinámica de las neuronas, típicas de la computación de reservorio, utilizando sistemas cuánticos. Esto es realmente un desafío y aún queda mucho por investigar. A pesar de ser un campo muy nuevo, empieza a haber estudios prometedores que indican una gran posible ventaja en términos de coste computacional en comparación con los métodos clásicos (Roberta Zambrini, 2021).
Bibliografía
Guillermo B. Morales, C. R. (2021). Unveiling the role of plasticity rules in reservoir computing. Neurocomputing , 705-715.
Miguel A Muñoz, G. B. (2021). Optimal input representation in neural systems at the edge of chaos. Biology , 702.
Mitsumasa Nakajima, K. T. (2021). Scalable reservoir computing on coherent linear photonic processor. Nature .
Roberta Zambrini, P. M.-P.-B. (2021). Opportunities in Quantum Reservoir Computing and Extreme Learning Machines. Adv. Quantum Technol.


