Colaboración de Daniel Montesinos Capacete ( Becario Sicómoro 23-24 del Máster del IFISC).
Introducción
La naturaleza es un constante escenario de transformaciones; en cada rincón, siempre podemos identificar algo que difiere del día anterior. A veces, estos cambios suceden lentamente, imperceptibles para el ojo humano, mientras que en otras ocasiones, se manifiestan de manera abrupta, provocando grandes transformaciones a partir de pequeñas disparidades.
Tomemos como ejemplo el comportamiento del agua. Todos sabemos que se solidifica por debajo de 0 ºC. Sin embargo, ¿implica esto que a 0.001 ºC tenemos agua líquida y, con una mínima variación a –0.001 ºC, obtenemos hielo puro? La respuesta a esta pregunta, en realidad, dependería de diversos factores, como la presión atmosférica y el proceso de calentamiento. No obstante, lo crucial aquí es comprender que modificaciones aparentemente insignificantes en los parámetros que definen un sistema pueden generar comportamientos completamente distintos, complicados de analizar.
Este fenómeno, conocido como transiciones de fases, se manifiesta en una variedad de sistemas físicos de naturaleza diversa. Otro ejemplo palpable de estas transiciones se observa en los imanes, que pueden perder sus propiedades magnéticas al aumentar considerablemente la temperatura, ingresando a una fase no magnética. Estos comportamientos macroscópicos son el resultado de las características microscópicas que subyacen en el sistema a nivel molecular.
Los fenómenos críticos y colectivos, desde la perspectiva de los sistemas complejos, constituyen un fascinante ámbito de estudio que se adentra en la interacción y emergencia de patrones a nivel colectivo. En este enfoque, se analizan sistemas compuestos por múltiples componentes interconectados, donde pequeñas perturbaciones pueden desencadenar cambios significativos y, a su vez, la colectividad influye en el comportamiento individual. Fenómenos como la sincronización, la autoorganización y la propagación de información muestran cómo las propiedades del sistema no son simplemente la suma de sus partes, sino el resultado de complejas interacciones no lineales. Este enfoque ofrece una visión profunda de cómo los sistemas complejos exhiben comportamientos críticos y colectivos, revelando patrones emergentes que van más allá de las características individuales de los componentes.
Para adentrarnos en el fascinante mundo de los fenómenos críticos y colectivos en sistemas complejos, exploraremos un modelo que nos lleva a un reino donde las serpientes se convierten en agentes de organización sin necesidad de “pegamento” (término de adherencia explícito). Este modelo se conoce como “flexible chainlike random walkers“. Sin embargo, para simplificar nuestra conversación y hacerla más accesible, nos referiremos a este modelo como “serpientes aleatorias“. Este término no solo simplifica la discusión, sino que también evoca una imagen visualmente sugerente: un conjunto de serpientes moviéndose de manera impredecible en un plano. El modelo fue propuesto por Takashi Mashiko en 2008 (Mashiko, 2008).
De forma general, el estudio de movimientos aleatorios en sistemas complejos es de gran interés, ya que permite comprender fenómenos como el movimiento de partículas suspendidas en un fluido (movimiento browniano), fundamental en campos como la física, la biología y la economía. Además, el caso específico del movimiento de serpientes aleatorias ofrece un enfoque único que podría tener futuras aplicaciones en el control de robots serpientes o en el estudio de comportamientos bacterianos. Con los avances recientes en robótica e inteligencia artificial, la posibilidad de utilizar robots serpientes para explorar zonas inaccesibles después de derrumbes o catástrofes naturales se vislumbra como una aplicación especialmente prometedora.
El concepto central de las “serpientes aleatorias” desafía nuestra concepción convencional acerca de cómo los elementos se unen para formar estructuras. Estas serpientes, al moverse de manera aleatoria, logran organizarse y ensamblarse sin requerir ningún tipo de fuerza adhesiva externa. Es como si cada serpiente fuera una pieza de un rompecabezas que encuentra su lugar en el conjunto de forma autónoma. Este enfoque nos permitirá examinar el comportamiento global de un conjunto de N serpientes, cada una de longitud l, moviéndose de manera aleatoria en un plano.
A continuación, se ofrece una breve descripción del sistema junto con algunas condiciones importantes a tener en cuenta. Luego, se ejemplifica la dinámica del sistema con dos ejemplos de movimiento aleatorio de serpientes. Una vez asentadas las bases del modelo, se detallan las magnitudes de interés y se presentan los resultados de varias simulaciones, donde se observa una transición de fase del sistema desde un estado de alta movilidad hasta uno de movilidad nula, similar a la transición del agua de estado sólido a líquido al aumentar la temperatura. Por último, se ofrecen algunas reflexiones y modelos más avanzados en la conclusión.
1. Descripción del Sistema
El sistema (es decir, el plano en el que se mueven las serpientes) se describe a partir de una matriz 𝑀 cuadrada 𝐿 x 𝐿 donde 𝐿 es un parámetro que modifica el tamaño del mismo. En general, una matriz se puede entender como un conjunto de números ordenados de manera que el elemento 𝑀ij hace referencia al número en la fila i y columna j. En nuestro modelo de serpientes aleatorias, para los huecos vacíos usamos 𝑀ij =0 mientras que para los ocupados por una parte de la serpiente utilizamos 𝑀ij =1. Esta idea se ve esquematizada en la Figura 1 donde se muestra un ejemplo para L=4 y l=4.
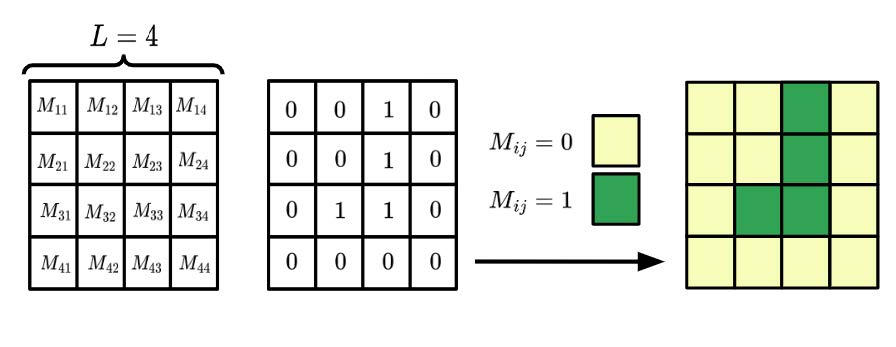
Figura 1: Esquema de la representación matricial del sistema para donde se ve como los elementos de matriz se pueden representar en una cuadrícula. Adicionalmente, se muestra un ejemplo de cómo se ve una serpiente de longitud utilizando un código de color.
La matriz que define el sistema es la base para realizar simulaciones numéricas del movimiento aleatorio de las serpientes. Sin embargo, es crucial abordar la situación en los bordes de nuestro sistema. ¿Qué sucede si una serpiente intenta desplazarse fuera de nuestra cuadrícula? En este contexto, es común emplear lo que se conoce como condiciones de contorno periódicas, cuyo concepto se ilustra en la Figura 2. La premisa aquí es visualizar que cada borde de la cuadrícula se extiende de manera continua hacia su borde opuesto, de modo que al abandonar la cuadrícula por la derecha, la serpiente regresaría a ingresar por la izquierda.
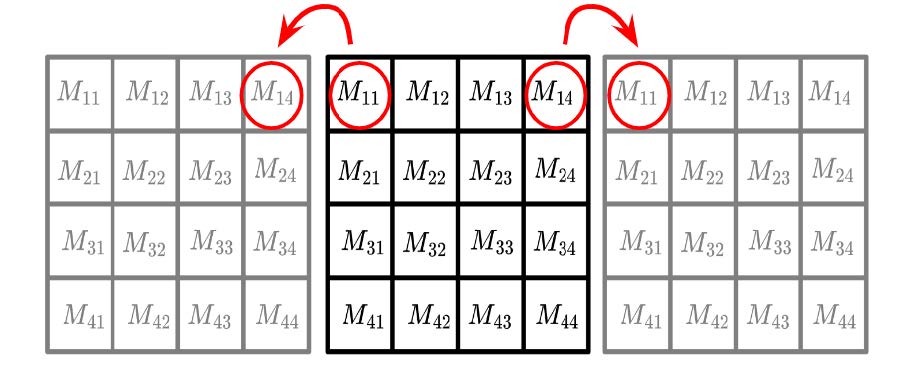
Figura 2: Representación gráfica del significado de las condiciones de contorno periódicas para la dirección horizontal. Si la cabeza de una serpiente está en la posición y decide moverse hacia la derecha, se está moviendo a la posición . Aunque no esté representado, lo mismo ocurre en la dirección vertical.
2. Descripción del Movimiento
Ahora que hemos establecido con claridad las características del sistema, procedamos a describir el modo en que se desplazan las serpientes. Cada una de estas está conformada por l huecos de la cuadrícula, y elegimos uno de los extremos de la serpiente como su cabeza. En cada intervalo de tiempo durante la simulación, la cabeza decide moverse aleatoriamente en una de las cuatro posibles direcciones: derecha, izquierda, arriba o abajo. Sin embargo, si el hueco al que intenta trasladarse está ocupado por ella misma u otra serpiente, se considera un intento fallido y la serpiente permanece en su posición actual.
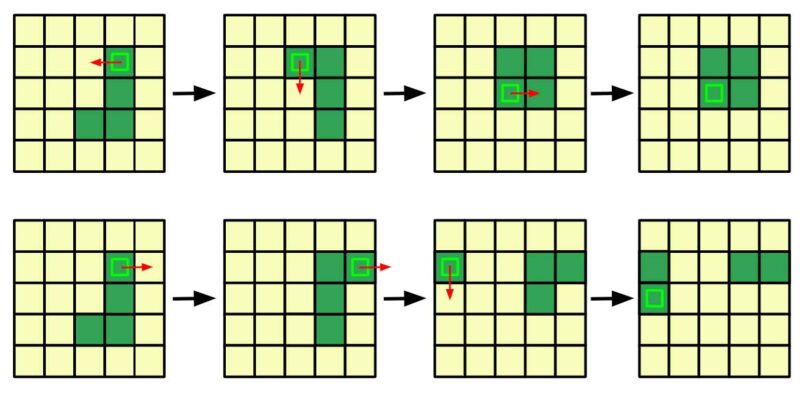
Figura 3: Representación de dos posibles trayectorias independientes para el movimiento de la serpiente. Su cabeza se ha representado con un pequeño recuadro verde claro de forma ilustrativa y la flecha roja indica la dirección de movimiento aleatorio a cada paso. Notar como la serpiente no se mueve si el hueco destino está ocupado (trayectoria superior) y el efecto de las condiciones de contorno periódicas (trayectoria inferior).
3. Magnitudes de Interés
Ya hemos conseguido describir las propiedades del sistema y el movimiento de las serpientes. Lo último que nos falta es concretar las propiedades de interés teniendo en cuenta que la idea es estudiar cómo cambia la dinámica de las serpientes frente a cambios en el sistema. Para ello, definimos la densidad del sistema como:
y la movilidad del sistema como:
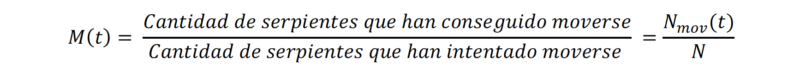
ya que todas las serpientes se intentan mover en cada tiempo. Así, nuestro propósito será examinar cómo varía la movilidad del sistema en relación con su densidad. De manera más específica, nos enfocaremos en observar cómo se modifica el valor de equilibrio de la movilidad, que definimos como: 
En la práctica, esto implica analizar el valor de la movilidad después de un período lo suficientemente extenso, durante el cual asumimos que la movilidad alcanza un estado constante, representado por M∞. De esta forma, se realizan simulaciones numéricas con el objetivo de calcular M∞ para diferentes densidades y distinto valor de la longitud l de las serpientes.
4. Resultados Numéricos
Los resultados de las simulaciones se muestran en la Figura 4 donde observamos que, para l=5 y l=6 , la movilidad M∞ es prácticamente nula desde el principio. Sin embargo, para l=3 y l=4 , se observa una dependencia más interesante. Para valores bajos de la densidad, la movilidad se mantiene alta pero al aumentar la densidad a partir de cierto valor obtenemos una movilidad nula. Esto que estamos observando es una transición de fase entre estas dos situaciones debido al cambio en la densidad de serpientes del sistema.
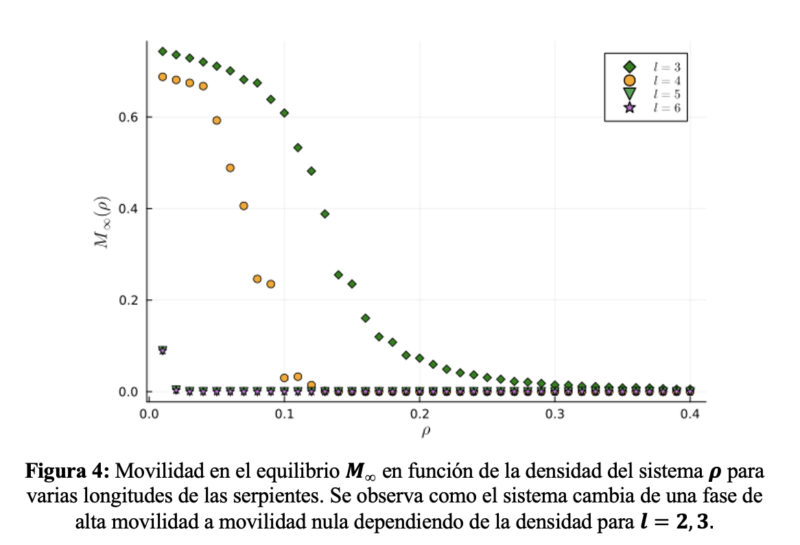
Estos resultados se pueden entender de la siguiente forma. Al aumentar el número de serpientes, hay mayor probabilidad de que se intenten mover a huecos ocupados y por lo tanto la movilidad se reduce. De hecho, es posible que varias serpientes se agrupen de forma que se bloquean por completo y ninguna pueda moverse más. Esto produce una formación espontánea de estructuras que emerge del movimiento aleatorio de las serpientes conforme se aumenta la densidad como se ve en la Figura 5.
En esta imagen estamos viendo la representación en color de la matriz del sistema en el estado de equilibrio para dos valores de la densidad diferentes. Mientras que para ρ=0.1, las serpientes siguen su movimiento aleatorio libremente, para ρ=0.3 se forman aglomeraciones de serpientes debido a que se bloquean entre ellas.
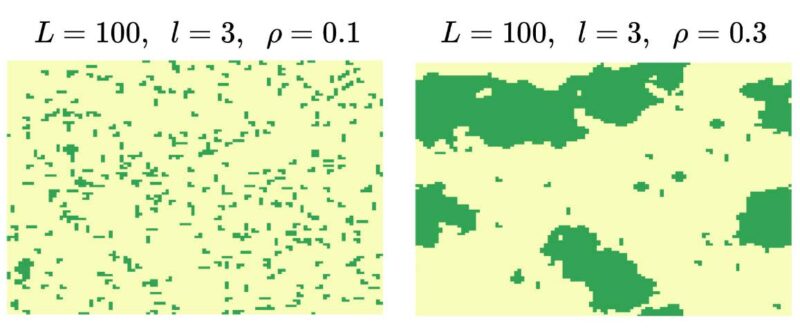
Figura 5: Representación gráfica del sistema en el estado de equilibrio para un mismo tamaño y longitud de serpiente pero diferentes densidades.
Así pues, hemos observado que en este modelo de serpientes aleatorias existe una densidad crítica específica que provoca alteraciones significativas en el comportamiento global del sistema. Este fenómeno da origen a dos fases claramente distinguibles, comúnmente denominadas como desordenada (en la cual las serpientes, en equilibrio, siguen movimientos completamente aleatorios) y ordenada (donde, en equilibrio, el sistema presenta una estructura concreta).
5. Conclusiones
Como hemos observado, las transiciones de fase son fenómenos comunes en una amplia variedad de sistemas físicos complejos, surgiendo de las interacciones entre sus componentes individuales. En nuestro estudio del sistema de serpientes aleatorias, hemos presenciado una transición de fase, destacando los efectos críticos colectivos asociados con cambios en su densidad, como fue presentado por Takashi Mashiko en 2008 (Mashiko, 2008). Aunque este modelo tiene menos de veinte años desde su propuesta inicial, las posibles aplicaciones son prometedoras. Por ejemplo, la adaptación de este modelo a robots tipo serpiente podría ser útil para crear barreras o para responder a emergencias como zonas inundadas. Imagínense nano-robots serpiente capaces de generar tejidos adaptables a partir de la autoorganización observada en este sistema. La imaginación para crear a partir de la ciencia no tiene límites.
En 2009, Takashi Mashiko amplió su investigación al agregar bidireccionalidad a las serpientes, permitiendo que tanto la cabeza como la cola elijan direcciones de movimiento. En este caso, observó que la formación espontánea de estructuras, previamente observada, ya no se producía (Takashi Mashiko Y. I., 2009).
Aunque este hallazgo sea esencialmente teórico, existe la posibilidad de complicar el modelo al dotar a las serpientes de inteligencia y comportamientos más complejos que el simple movimiento aleatorio. Otro estudio se ha realizado explorando estas modificaciones con el objetivo de analizar el flujo de tráfico y fenómenos de congestión. En ese trabajo se explora como el movimiento de serpientes aleatorias movidas por un cierto término de arrastre y sin obstáculos, dan lugar a un movimiento unidireccional pero con una transición de fase a un estado de bloqueo total (Takashi Mashiko Y. I., 2009). Este fenómeno de bloqueo total es algo así como un “congelamiento” en el movimiento de estos objetos. Es como si, de repente, las serpientes robóticas o las bacterias dejaran de moverse por completo. Lo más interesante es que esto no se había observado antes en flujos unidireccionales sin obstáculos. Esto nos lleva a pensar en aplicaciones prácticas intrigantes. ¿Imaginas serpientes robóticas que, al volverse flexibles, podrían bloquearse estratégicamente para crear barreras temporales en ciertos lugares? Este hallazgo también puede tener implicaciones en la automatización de fábricas y el diseño de robots más adaptables y versátiles.
Algunos estudios más recientes han considerado la posibilidad de añadir cierta deformabilidad a las cadenas que forman las serpientes, lo que da lugar a comportamientos y transiciones de fases diferentes a las que hemos visto (Takashi Mashiko Y. F., 2016). En este caso, las serpientes aleatorias se desplazan en un espacio bidimensional sin restricciones (no son obligadas a seguir una cuadrícula). La sorpresa radica en que estos objetos, sin importar si son flexibles o no, tienden a unirse espontáneamente de manera irreversible. Esto se destaca en comparación con situaciones en las que están confinados a una cuadrícula, donde la unión solo ocurre si son flexibles. Además, se ve que la propensión a unirse aumenta cuando estos objetos son menos flexibles o experimentan más fluctuaciones. Comprender este tipo de fenómeno podría ser interesante para mejorar flujos o crear estructuras inteligentes.
En la parte experimental, se pueden encontrar fenómenos de bloqueos entre partículas de forma parecida al caso de las serpientes aleatorias. En el estudio realizado por Emily A. y otros en 2020, se explora el fenómeno de atasco en un flujo bidireccional de partículas a través de un tubo, sin la presencia de constricciones físicas (Emily A. Hobbs, 2020). Al utilizar partículas de diferentes densidades en un fluido, se observa que el atasco ocurría de manera inesperada. La probabilidad de atasco exhibió una transición crítica en la densidad similar al caso de las serpientes aleatorias. Estos resultados desafían las expectativas convencionales, destacando las complejas interacciones entre las partículas en una geometría aparentemente simple al igual que ocurría con nuestro modelo de serpientes aleatorias.
6. Bibliografía
Emily A. Hobbs, A. C. (2020). Clogging in bidirectional suspension flow. arXiv preprint arXiv:2003.06102 .
Mashiko, T. (2009). Effect of Individual Properties of Flexible Chainlike Walkers in a ManyBody System. The Open Transport Phenomena Journal , 30-34.
Mashiko, T. (2008). Irreversible aggregation of flexible chainlike walkers without adherence. Physical Review .
Takashi Mashiko, Y. F. (2016). Aggregation of Flexible Chainlike Walkers in Off-Lattice Space . Journal of Computer Science & Computational Mathematics .
Takashi Mashiko, Y. I. (2009). Hardening by softening in a flow of chainlike self-driven objects. Physica A .
Introducción
La naturaleza es un constante escenario de transformaciones; en cada rincón, siempre podemos identificar algo que difiere del día anterior. A veces, estos cambios suceden lentamente, imperceptibles para el ojo humano, mientras que en otras ocasiones, se manifiestan de manera abrupta, provocando grandes transformaciones a partir de pequeñas disparidades.
Tomemos como ejemplo el comportamiento del agua. Todos sabemos que se solidifica por debajo de 0 ºC. Sin embargo, ¿implica esto que a 0.001 ºC tenemos agua líquida y, con una mínima variación a –0.001 ºC, obtenemos hielo puro? La respuesta a esta pregunta, en realidad, dependería de diversos factores, como la presión atmosférica y el proceso de calentamiento. No obstante, lo crucial aquí es comprender que modificaciones aparentemente insignificantes en los parámetros que definen un sistema pueden generar comportamientos completamente distintos, complicados de analizar.
Este fenómeno, conocido como transiciones de fases, se manifiesta en una variedad de sistemas físicos de naturaleza diversa. Otro ejemplo palpable de estas transiciones se observa en los imanes, que pueden perder sus propiedades magnéticas al aumentar considerablemente la temperatura, ingresando a una fase no magnética. Estos comportamientos macroscópicos son el resultado de las características microscópicas que subyacen en el sistema a nivel molecular.
Los fenómenos críticos y colectivos, desde la perspectiva de los sistemas complejos, constituyen un fascinante ámbito de estudio que se adentra en la interacción y emergencia de patrones a nivel colectivo. En este enfoque, se analizan sistemas compuestos por múltiples componentes interconectados, donde pequeñas perturbaciones pueden desencadenar cambios significativos y, a su vez, la colectividad influye en el comportamiento individual. Fenómenos como la sincronización, la autoorganización y la propagación de información muestran cómo las propiedades del sistema no son simplemente la suma de sus partes, sino el resultado de complejas interacciones no lineales. Este enfoque ofrece una visión profunda de cómo los sistemas complejos exhiben comportamientos críticos y colectivos, revelando patrones emergentes que van más allá de las características individuales de los componentes.
Para adentrarnos en el fascinante mundo de los fenómenos críticos y colectivos en sistemas complejos, exploraremos un modelo que nos lleva a un reino donde las serpientes se convierten en agentes de organización sin necesidad de “pegamento” (término de adherencia explícito). Este modelo se conoce como “flexible chainlike random walkers“. Sin embargo, para simplificar nuestra conversación y hacerla más accesible, nos referiremos a este modelo como “serpientes aleatorias“. Este término no solo simplifica la discusión, sino que también evoca una imagen visualmente sugerente: un conjunto de serpientes moviéndose de manera impredecible en un plano. El modelo fue propuesto por Takashi Mashiko en 2008 (Mashiko, 2008).
De forma general, el estudio de movimientos aleatorios en sistemas complejos es de gran interés, ya que permite comprender fenómenos como el movimiento de partículas suspendidas en un fluido (movimiento browniano), fundamental en campos como la física, la biología y la economía. Además, el caso específico del movimiento de serpientes aleatorias ofrece un enfoque único que podría tener futuras aplicaciones en el control de robots serpientes o en el estudio de comportamientos bacterianos. Con los avances recientes en robótica e inteligencia artificial, la posibilidad de utilizar robots serpientes para explorar zonas inaccesibles después de derrumbes o catástrofes naturales se vislumbra como una aplicación especialmente prometedora.
El concepto central de las “serpientes aleatorias” desafía nuestra concepción convencional acerca de cómo los elementos se unen para formar estructuras. Estas serpientes, al moverse de manera aleatoria, logran organizarse y ensamblarse sin requerir ningún tipo de fuerza adhesiva externa. Es como si cada serpiente fuera una pieza de un rompecabezas que encuentra su lugar en el conjunto de forma autónoma. Este enfoque nos permitirá examinar el comportamiento global de un conjunto de N serpientes, cada una de longitud l, moviéndose de manera aleatoria en un plano.
A continuación, se ofrece una breve descripción del sistema junto con algunas condiciones importantes a tener en cuenta. Luego, se ejemplifica la dinámica del sistema con dos ejemplos de movimiento aleatorio de serpientes. Una vez asentadas las bases del modelo, se detallan las magnitudes de interés y se presentan los resultados de varias simulaciones, donde se observa una transición de fase del sistema desde un estado de alta movilidad hasta uno de movilidad nula, similar a la transición del agua de estado sólido a líquido al aumentar la temperatura. Por último, se ofrecen algunas reflexiones y modelos más avanzados en la conclusión.
1. Descripción del Sistema
El sistema (es decir, el plano en el que se mueven las serpientes) se describe a partir de una matriz 𝑀 cuadrada 𝐿 x 𝐿 donde 𝐿 es un parámetro que modifica el tamaño del mismo. En general, una matriz se puede entender como un conjunto de números ordenados de manera que el elemento 𝑀ij hace referencia al número en la fila i y columna j. En nuestro modelo de serpientes aleatorias, para los huecos vacíos usamos 𝑀ij =0 mientras que para los ocupados por una parte de la serpiente utilizamos 𝑀ij =1. Esta idea se ve esquematizada en la Figura 1 donde se muestra un ejemplo para L=4 y l=4.
Figura 1: Esquema de la representación matricial del sistema para donde se ve como los elementos de matriz se pueden representar en una cuadrícula. Adicionalmente, se muestra un ejemplo de cómo se ve una serpiente de longitud utilizando un código de color.
La matriz que define el sistema es la base para realizar simulaciones numéricas del movimiento aleatorio de las serpientes. Sin embargo, es crucial abordar la situación en los bordes de nuestro sistema. ¿Qué sucede si una serpiente intenta desplazarse fuera de nuestra cuadrícula? En este contexto, es común emplear lo que se conoce como condiciones de contorno periódicas, cuyo concepto se ilustra en la Figura 2. La premisa aquí es visualizar que cada borde de la cuadrícula se extiende de manera continua hacia su borde opuesto, de modo que al abandonar la cuadrícula por la derecha, la serpiente regresaría a ingresar por la izquierda.
Figura 2: Representación gráfica del significado de las condiciones de contorno periódicas para la dirección horizontal. Si la cabeza de una serpiente está en la posición y decide moverse hacia la derecha, se está moviendo a la posición . Aunque no esté representado, lo mismo ocurre en la dirección vertical.
2. Descripción del Movimiento
Ahora que hemos establecido con claridad las características del sistema, procedamos a describir el modo en que se desplazan las serpientes. Cada una de estas está conformada por l huecos de la cuadrícula, y elegimos uno de los extremos de la serpiente como su cabeza. En cada intervalo de tiempo durante la simulación, la cabeza decide moverse aleatoriamente en una de las cuatro posibles direcciones: derecha, izquierda, arriba o abajo. Sin embargo, si el hueco al que intenta trasladarse está ocupado por ella misma u otra serpiente, se considera un intento fallido y la serpiente permanece en su posición actual.
Figura 3: Representación de dos posibles trayectorias independientes para el movimiento de la serpiente. Su cabeza se ha representado con un pequeño recuadro verde claro de forma ilustrativa y la flecha roja indica la dirección de movimiento aleatorio a cada paso. Notar como la serpiente no se mueve si el hueco destino está ocupado (trayectoria superior) y el efecto de las condiciones de contorno periódicas (trayectoria inferior).
3. Magnitudes de Interés
Ya hemos conseguido describir las propiedades del sistema y el movimiento de las serpientes. Lo último que nos falta es concretar las propiedades de interés teniendo en cuenta que la idea es estudiar cómo cambia la dinámica de las serpientes frente a cambios en el sistema. Para ello, definimos la densidad del sistema como:
y la movilidad del sistema como:
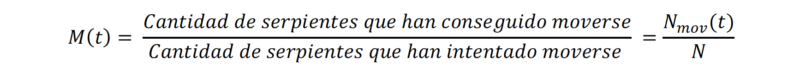
ya que todas las serpientes se intentan mover en cada tiempo. Así, nuestro propósito será examinar cómo varía la movilidad del sistema en relación con su densidad. De manera más específica, nos enfocaremos en observar cómo se modifica el valor de equilibrio de la movilidad, que definimos como: En la práctica, esto implica analizar el valor de la movilidad después de un período lo suficientemente extenso, durante el cual asumimos que la movilidad alcanza un estado constante, representado por M∞. De esta forma, se realizan simulaciones numéricas con el objetivo de calcular M∞ para diferentes densidades y distinto valor de la longitud l de las serpientes.
4. Resultados Numéricos
Los resultados de las simulaciones se muestran en la Figura 4 donde observamos que, para l=5 y l=6 , la movilidad M∞ es prácticamente nula desde el principio. Sin embargo, para l=3 y l=4 , se observa una dependencia más interesante. Para valores bajos de la densidad, la movilidad se mantiene alta pero al aumentar la densidad a partir de cierto valor obtenemos una movilidad nula. Esto que estamos observando es una transición de fase entre estas dos situaciones debido al cambio en la densidad de serpientes del sistema.
Estos resultados se pueden entender de la siguiente forma. Al aumentar el número de serpientes, hay mayor probabilidad de que se intenten mover a huecos ocupados y por lo tanto la movilidad se reduce. De hecho, es posible que varias serpientes se agrupen de forma que se bloquean por completo y ninguna pueda moverse más. Esto produce una formación espontánea de estructuras que emerge del movimiento aleatorio de las serpientes conforme se aumenta la densidad como se ve en la Figura 5.
En esta imagen estamos viendo la representación en color de la matriz del sistema en el estado de equilibrio para dos valores de la densidad diferentes. Mientras que para ρ=0.1, las serpientes siguen su movimiento aleatorio libremente, para ρ=0.3 se forman aglomeraciones de serpientes debido a que se bloquean entre ellas.
Figura 5: Representación gráfica del sistema en el estado de equilibrio para un mismo tamaño y longitud de serpiente pero diferentes densidades.
Así pues, hemos observado que en este modelo de serpientes aleatorias existe una densidad crítica específica que provoca alteraciones significativas en el comportamiento global del sistema. Este fenómeno da origen a dos fases claramente distinguibles, comúnmente denominadas como desordenada (en la cual las serpientes, en equilibrio, siguen movimientos completamente aleatorios) y ordenada (donde, en equilibrio, el sistema presenta una estructura concreta).
5. Conclusiones
Como hemos observado, las transiciones de fase son fenómenos comunes en una amplia variedad de sistemas físicos complejos, surgiendo de las interacciones entre sus componentes individuales. En nuestro estudio del sistema de serpientes aleatorias, hemos presenciado una transición de fase, destacando los efectos críticos colectivos asociados con cambios en su densidad, como fue presentado por Takashi Mashiko en 2008 (Mashiko, 2008). Aunque este modelo tiene menos de veinte años desde su propuesta inicial, las posibles aplicaciones son prometedoras. Por ejemplo, la adaptación de este modelo a robots tipo serpiente podría ser útil para crear barreras o para responder a emergencias como zonas inundadas. Imagínense nano-robots serpiente capaces de generar tejidos adaptables a partir de la autoorganización observada en este sistema. La imaginación para crear a partir de la ciencia no tiene límites.
En 2009, Takashi Mashiko amplió su investigación al agregar bidireccionalidad a las serpientes, permitiendo que tanto la cabeza como la cola elijan direcciones de movimiento. En este caso, observó que la formación espontánea de estructuras, previamente observada, ya no se producía (Takashi Mashiko Y. I., 2009).
Aunque este hallazgo sea esencialmente teórico, existe la posibilidad de complicar el modelo al dotar a las serpientes de inteligencia y comportamientos más complejos que el simple movimiento aleatorio. Otro estudio se ha realizado explorando estas modificaciones con el objetivo de analizar el flujo de tráfico y fenómenos de congestión. En ese trabajo se explora como el movimiento de serpientes aleatorias movidas por un cierto término de arrastre y sin obstáculos, dan lugar a un movimiento unidireccional pero con una transición de fase a un estado de bloqueo total (Takashi Mashiko Y. I., 2009). Este fenómeno de bloqueo total es algo así como un “congelamiento” en el movimiento de estos objetos. Es como si, de repente, las serpientes robóticas o las bacterias dejaran de moverse por completo. Lo más interesante es que esto no se había observado antes en flujos unidireccionales sin obstáculos. Esto nos lleva a pensar en aplicaciones prácticas intrigantes. ¿Imaginas serpientes robóticas que, al volverse flexibles, podrían bloquearse estratégicamente para crear barreras temporales en ciertos lugares? Este hallazgo también puede tener implicaciones en la automatización de fábricas y el diseño de robots más adaptables y versátiles.
Algunos estudios más recientes han considerado la posibilidad de añadir cierta deformabilidad a las cadenas que forman las serpientes, lo que da lugar a comportamientos y transiciones de fases diferentes a las que hemos visto (Takashi Mashiko Y. F., 2016). En este caso, las serpientes aleatorias se desplazan en un espacio bidimensional sin restricciones (no son obligadas a seguir una cuadrícula). La sorpresa radica en que estos objetos, sin importar si son flexibles o no, tienden a unirse espontáneamente de manera irreversible. Esto se destaca en comparación con situaciones en las que están confinados a una cuadrícula, donde la unión solo ocurre si son flexibles. Además, se ve que la propensión a unirse aumenta cuando estos objetos son menos flexibles o experimentan más fluctuaciones. Comprender este tipo de fenómeno podría ser interesante para mejorar flujos o crear estructuras inteligentes.
En la parte experimental, se pueden encontrar fenómenos de bloqueos entre partículas de forma parecida al caso de las serpientes aleatorias. En el estudio realizado por Emily A. y otros en 2020, se explora el fenómeno de atasco en un flujo bidireccional de partículas a través de un tubo, sin la presencia de constricciones físicas (Emily A. Hobbs, 2020). Al utilizar partículas de diferentes densidades en un fluido, se observa que el atasco ocurría de manera inesperada. La probabilidad de atasco exhibió una transición crítica en la densidad similar al caso de las serpientes aleatorias. Estos resultados desafían las expectativas convencionales, destacando las complejas interacciones entre las partículas en una geometría aparentemente simple al igual que ocurría con nuestro modelo de serpientes aleatorias.
6. Bibliografía
Emily A. Hobbs, A. C. (2020). Clogging in bidirectional suspension flow. arXiv preprint arXiv:2003.06102 .
Mashiko, T. (2009). Effect of Individual Properties of Flexible Chainlike Walkers in a ManyBody System. The Open Transport Phenomena Journal , 30-34.
Mashiko, T. (2008). Irreversible aggregation of flexible chainlike walkers without adherence. Physical Review .
Takashi Mashiko, Y. F. (2016). Aggregation of Flexible Chainlike Walkers in Off-Lattice Space . Journal of Computer Science & Computational Mathematics .
Takashi Mashiko, Y. I. (2009). Hardening by softening in a flow of chainlike self-driven objects. Physica A .
