Colaboración especial de Joan Cucurull Benet ( Becario Sicómoro en el Máster del IFISC 2024-2025)
1. INTRODUCCIÓN Y CONTEXTO
La desertificación es una conocida consecuencia del cambio climático. El caso paradigmático de desertificación ocurre cuando en un territorio se reduce la cantidad de precipitación y las plantas que allí habitan, al no tener suficiente agua para sobrevivir, acaban muriendo y con ellas también el ecosistema que de ellas se alimenta. No obstante, este no es el único mecanismo por el cual un territorio puede desertificarse. El fondo marino también puede sufrir un proceso de desertificación, ¡y no es por falta de agua! Es el caso, por ejemplo, de las praderas marinas de posidonia oceánica en el Mediterráneo.
Las praderas marinas ofrecen ecosistemas esenciales que benefician la salud humana, los medios de vida y el bienestar general [2]. Su estructura compleja favorece la biodiversidad costera, proporciona alimento a las comunidades locales y da apoyo tanto a la pesca comercial como a la de subsistencia. Además, actúan como defensas costeras naturales contra la erosión. Las praderas marinas también contribuyen a mantener aguas oxigenadas, con bajos niveles de nutrientes y CO2, fijando cantidades significativas de carbono [3]. Sin embargo, desde mediados del siglo XX, aproximadamente un tercio de las praderas marinas del mundo han desaparecido por diversas razones, como el aumento de la temperatura del agua o la presencia de químicos fruto de la actividad humana [1].
2. MODELOS MATEMÁTICOS
Viendo estos datos, está claro que hay que encontrar herramientas teóricas que nos ayuden a entender las causas y evolución de estos procesos. Siendo aquí de donde surge la idea de utilizar modelos matemáticos para poder describir los procesos de desertificación. La física de los sistemas complejos puede proporcionarnos los modelos necesarios.
Los sistemas complejos son aquellos formados por numerosos componentes que interactúan entre sí con un alto grado de interconexión y comportamiento emergente. A menudo muestran patrones y fenómenos intrincados que no se pueden predecir a partir del conocimiento de los componentes individuales.
Este es el caso de la Posidonia oceánica, un organismo vegetal formado por individuos que se reproducen principalmente por clonación (como muchas otras plantas). Este proceso de reproducción tiene factores que lo favorecen y factores limitantes. La reproducción por clonación en praderas marinas se puede simular utilizando modelos de crecimiento estadísticos [6]. Estos modelos de crecimiento son simulaciones microscópicas, individuo a individuo. No obstante, existen otros métodos dentro de la física de los sistemas complejos que nos permiten simular las praderas marinas a nivel macroscópico, como conjunto homogéneo de biomasa, y no como partículas individuales. Esta forma de abordar el problema nos dará resultados más universales y aplicables a todo tipo de ecosistemas vegetales.
Es el caso de la dinámica espacio-temporal, una rama de los sistemas complejos que permite modelar la evolución de las cubiertas vegetales de los ecosistemas en función de los cambios en su entorno. Este enfoque consiste en encontrar la ecuación de evolución temporal de la biomasa de un ecosistema vegetal a lo largo del espacio, en función de parámetros relacionados con factores ecológicos como la cantidad anual de lluvia, la temperatura del agua (en el caso de los ecosistemas marinos), la presencia de químicos, o incluso un parámetro que agrupe los factores más determinantes, para simplificar el estudio del sistema.
La ecuación de la cantidad de masa vegetal se escribe como un balance entre los procesos que favorecen la presencia vegetal y los procesos que la reducen, como puede ser la competencia por nutrientes del entorno. Una vez determinada la ecuación que describe la evolución del sistema, se trata de encontrar, en función de los valores de los parámetros, cuáles son las soluciones estables.
El modelo clásico para abordar este problema consiste en considerar que la vegetación cubre homogéneamente el suelo disponible. En el caso más prototípico, el resultado del análisis de estabilidad se representa en la siguiente figura:
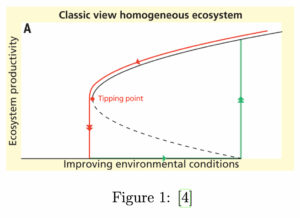
En este gráfico, las soluciones estables (masa vegetal en función de un parámetro ecológico) están representadas por líneas continuas, y las inestables (que no nos interesan en este análisis) por líneas discontinuas. Variando el parámetro ecológico, podemos ver que el proceso de desertificación se produce de forma abrupta a partir de un determinado umbral llamado tipping point (punto de inflexión), trayectoria roja en el gráfico.
Por ejemplo: Supongamos una superficie vegetal terrestre. Aquí, el parámetro que el gráfico llama ”mejora de condiciones ambientales” podría ser la cantidad de lluvia. Así, este modelo nos dice que una vez el territorio se desertifica a partir de una cantidad crítica de lluvia, no basta con volver a superar esta precipitación crítica para revertir el proceso. Es necesario aumentar la precipitación hasta alcanzar un nuevo valor crítico, más alto que el anterior, a partir del cual se puede repoblar la vegetación (trayectoria verde en el gráfico).
Esto ocurre porque el modelo recoge una característica típica de los sistemas vegetales: la presencia de vegetación fija el suelo y favorece la presencia de más vegetación. La cantidad de lluvia necesaria para que se produzca la fijación de plantas en el suelo es mayor que la necesaria para que las plantas sobrevivan en un suelo ya fijado.
Este modelo predice que la desertificación es más irreversible de lo que podríamos haber previsto, debido al efecto de la fijación del suelo. Este resultado es intuitivo y se ha observado en muchas situaciones diferentes. No obstante, se han observado casos de superficies vegetales con mecanismos de resiliencia que permiten evitar los umbrales expuestos anteriormente. Este mecanismo de resiliencia consiste en formar patrones espaciales de vegetación: franjas de suelo cubiertas junto con franjas descubiertas situadas periódicamente. Esto permite tener zonas de suelo fijado, con mayor abundancia de recursos externos (como minerales) gracias a las franjas sin vegetación. Por tanto, abandonamos la suposición del modelo anterior, que solo consideraba superficies homogéneamente cubiertas por vegetación. Haciendo el análisis de estabilidad con el nuevo modelo, la figura 1 se modifica como vemos en el siguiente gráfico:
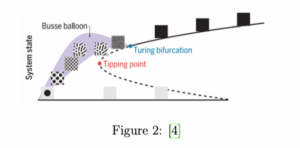
Como vemos en esta figura, el nuevo modelo predice una evasión del ”tipping point”, generando un conjunto de soluciones estables dentro de una región paramétrica llamada ”Busse balloon”, que comienza en un punto llamado ”bifurcación de Turing”, que es el punto a partir del cual la vegetación deja de ser homogénea y comienza a formar patrones.[4]
3. APLICACIÓN DEL MODELO A UN CASO REAL
La isla de Mallorca se encuentra en medio del Mediterráneo, rodeada de praderas de posidonia. La forma de estas praderas marinas puede verse por satélite en algunos puntos de la costa de la isla. Las imágenes tomadas por satélites de la Bahía de Pollença revelan una pradera marina no homogénea con patrones que recuerdan a la piel de un leopardo:
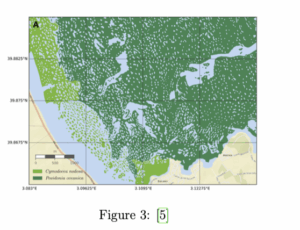
Estos resultados pueden explicarse a partir del modelo matemático expuesto en el apartado anterior, tal como se hizo por primera vez en el Instituto de Física Interdisciplinaria y Sistemas Complejos (IFISC) en Mallorca en el año 2017. Expliquémoslo: la ecuación de la biomasa de la posidonia es la del modelo ABD (”Advection-Branching-Death”) [5], una ecuación diferencial de la densidad de tallos de posidonia en función del espacio y de parámetros ecológicos relacionados con el modelo de crecimiento por clonación. La ecuación deriva directamente de los mecanismos microscópicos implicados en el crecimiento de plantas clonales, concretamente el alargamiento de los rizomas (que aparece en el modelo como un término de advección), la ramificación y la muerte, y sus parámetros pueden vincularse directamente a tasas y cantidades medidas en praderas submarinas. Las interacciones entre individuos también se recogen en esta ecuación (la competencia por nutrientes entre individuos y el favorecimiento de la presencia vegetal cuando los suelos ya están fijados por otros individuos). Estas interacciones son de largo alcance. Los resultados del análisis de estabilidad de la ecuación de densidad vegetal (¯ nt) están representados en la siguiente figura:
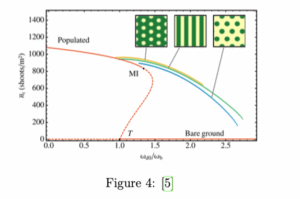
ωd0/ωb es un cociente de parámetros relacionados con el modelo de crecimiento clonal, que varían en función de las condiciones ambientales. El empeoramiento de las condiciones ambientales es equivalente al aumento del valor de este cociente. Vemos que los patrones de posidonia de la Bahía de Pollença son una solución de la ecuación del modelo (el conjunto de soluciones representado por la línea amarilla del gráfico), e indican que esta pradera de posidonia está entrando en un estado de estrés ambiental.
4. CONCLUSIONES
Modelizar significa encontrar un modelo matemático para reproducir un sistema real. La física de los sistemas complejos nos ha dotado de técnicas matemáticas que permiten modelar los procesos de desertificación del suelo terrestre (tanto en tierra como en el mar). Una vez encontrado el modelo, podemos utilizarlo para analizar en qué fase se encuentra un sistema vegetal y saber si está al límite de la desertificación. Esto es muy útil para dosificar inteligentemente los recursos que se aplican para mantener una cubierta vegetal en un suelo semiárido.
Pero yendo más allá, este conocimiento también puede ser una guía para restaurar suelos desertificados. Sabiendo los parámetros ecológicos de una región desértica, con el modelo expuesto en este artículo, se puede conocer cuál es el patrón de vegetación más estable en sus condiciones. De este modo, si se lleva a cabo una replantación, tendrá muchas más garantías de éxito.
En resumen, en una situación de cambio climático en todo nuestro planeta, los modelos que nos aporta la física de los sistemas complejos pueden ayudarnos a predecir y paliar los efectos ambientales sobre los ecosistemas vegetales.
REFERENCIAS
[1] Carlos Duarte et al. “The role of coastal plant communities for climate change mit igation and adaptation”. In: Nature Climate Change 3 (Nov. 2013), pp. 961–968. doi: 10.1038/nclimate1970.
[2] Rashid Hassan et al. Ecosystems and Human Well-Being: Current State and Trends: Findings of the Condition and Trends Working Group (Millennium Ecosystem Assessment Series). Jan. 2005.
[3] Elizabeth Mcleod. “A blueprint for blue carbon: Toward an improved understanding of the role of vegetated coastal habitats in sequestering CO2”. In: Front. Ecol. Environ 7 (Jan. 2011), pp. 362–370.
[4] Max Rietkerk et al. “Evasion of tipping in complex systems through spatial pattern formation”. In: Science 374.6564 (2021), eabj0359. doi: 10.1126/science.abj0359. eprint: https://www.science.org/doi/pdf/10.1126/science.abj0359. url: https://www.science.org/doi/abs/10.1126/science.abj0359.
[5] Daniel Ruiz-Reyn´es et al. “Fairy circle landscapes under the sea”. In: Science Advances 3.8 (2017), e1603262. doi: 10.1126/sciadv.1603262. eprint: https://www.science.org/doi/pdf/10.1126/sciadv.1603262. url: https://www.science.org/doi/abs/10.1126/sciadv.1603262.
[6] Tomás Sintes et al. “Nonlinear processes in seagrass colonisation explained by simple clonal growth rules”. In: Oikos 108 (Jan. 2005), pp. 165–175. doi: 10.1111/j.0030-1299.2005.13331.x.


